Medium
1M
192
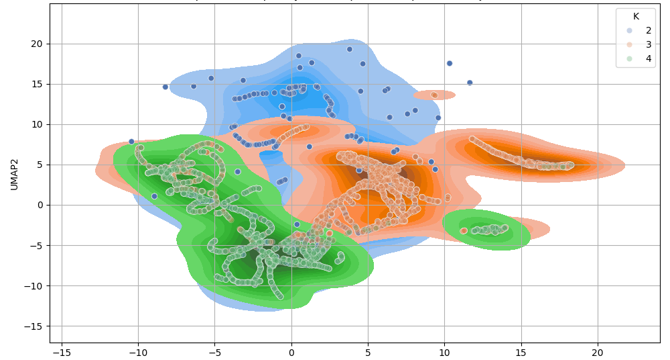
Image Credit: Medium
Clause-Arity and the Spectral Manifold of Complexity: Mapping the Geometry of SAT Solvability
- Over 5,000 labeled CNF formulas were generated and analyzed for SAT solvability using spectral features and UMAP projection.
- Satisfiable and unsatisfiable instances across different clause lengths were found to be separable in spectral space, indicating a general phenomenon.
- The dynamic match rule, utilizing μ ± σ thresholding, identifies the 'spectral core' of solvable problems across various clause types.
- The complexity landscape of SAT was visualized as a topological structure in a UMAP projection, suggesting new perspectives on P vs NP complexity classes.
Read Full Article
11 Likes
For uninterrupted reading, download the app