Dev
1w
388
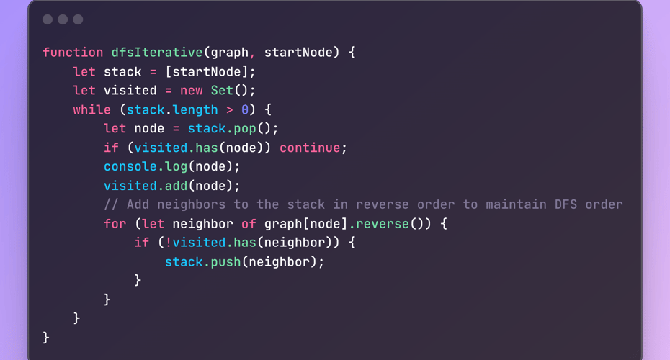
Image Credit: Dev
Converting Recursion to Iteration Using a Stack: A Practical Guide
- Recursion is a powerful technique in computer science, often used for tasks like tree traversal, depth-first search, and backtracking algorithms. However, recursion can be less efficient in terms of both time and space due to the overhead of function calls and maintaining the call stack. In some cases, it’s beneficial to convert recursion to an iterative approach using an explicit stack to simulate the recursive calls.
- There are several reasons why you might want to convert recursion to iteration:
- When converting a recursive function to an iterative one using a stack, the general approach remains similar across different types of algorithms (like tree traversals, backtracking problems, or graph traversal). Below is a flexible template that can be adapted to various scenarios.
- The stack should be initialized with the starting state, which could be the initial arguments or the first node in a traversal.
- In recursion, the base condition checks if further recursion is necessary. In the iterative approach, you can perform the same check inside the loop. You may use continue to skip further processing when the base condition is met.
- Process the state of the current iteration (equivalent to the processing that would occur at the current recursive call).
- This iterative version uses the stack to store the current state of the permutation. The backtracking is handled by pushing and popping the states from the stack.
- Converting recursion to iteration using a stack is a valuable technique for many algorithms, especially those involving backtracking or tree/graph traversal. By using an explicit stack, we can avoid deep recursion, manage function states manually, and ensure that we have better control over the algorithm’s execution. These examples should serve as a guide to help you tackle similar problems in your own code.
Read Full Article
23 Likes
For uninterrupted reading, download the app