Prodevelopertutorial
2w
87
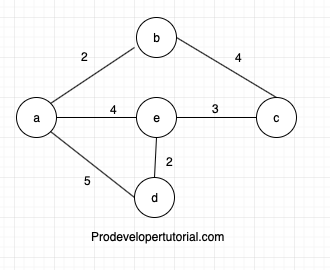
Image Credit: Prodevelopertutorial
Finding shortest path algorithm tutorial 2. Introduction to Dijkstra’s Algorithm
- Dijkstra’s algorithm is used to get single source shortest path algorithm.
- To solve this, we can generate all the possible paths from the source vertex to every other vertex. Find the weight of all the paths, compare those weights and find min of all those weights. This can be optimized using Dijkstra’s algorithm. Dijkstra’s algorithm is a greedy algorithm.
- All the edges should have positive weight. The graph should also be connected for the algorithm to work.
- Steps to perform Dijkstra’s algorithm: Step 1: Select any vertex as starting vertex. Step 2: Make the distance for all other vertices as INF. Step 3: From the starting vertex, visit all its adjacent/ neighbouring vertices and write their cost/value.
- Now that we have finished visiting all the adjacent vertices, we make the source vertex as visited. Choose another vertex, such that, the distance from source vertex is minimum.
- Consider 'u' as the source vertex. 'v' as the destination vertex. If distance(u) + cost of path(u,v) < distance_at(v), then distance(v) = distance_at(u) + cost of path(u, v).
- Example of implementing Dijkstra’s algorithm is provided in the article
- The article provides implementation of Dijkstra's algorithm using C++ programming language.
- The graph should have the properties like directed and undirected graphs, all edges should have positive weight, and should be connected.
- The Relaxation is the process of choosing the length of the new path form source vertex to destination vertex which is lesser than the current value, then update with the shortest value.
Read Full Article
5 Likes
For uninterrupted reading, download the app