Prodevelopertutorial
2w
388
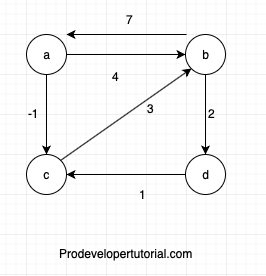
Image Credit: Prodevelopertutorial
Floyd Warshalls algorithm
- This tutorial discusses Floyd-Warshall's algorithm which is used to find the shortest path between all pairs of vertices in a graph.
- The algorithm is based on dynamic programming approach. It is the third type of algorithm to find the shortest path for all vertex to every other vertex.
- The article discusses previous two algorithms: Dijkstra's algorithm for finding the shortest path from one node to all other nodes/vertices and Bellman Ford's Algorithm to find the shortest path from one node to all other nodes.
- Based on DP approach, the algorithm finds the shortest path by breaking the problem into simple sub-problems and solving them.
- This article explains the algorithm using an example graph and by constructing distance matrices to solve the problem.
- The article also provides implementation details using a C program with steps to calculate the shortest path between all pairs of vertices in a graph.
- The output of the Floyd Warshall's algorithm is a shortest path matrix that provides the shortest distance between pairs of vertices in the graph.
- The algorithm works for both undirected and directed graphs and can handle negative edge weights.
- The time complexity of the algorithm is O(V^3), where V is the number of vertices in the graph.
- Floyd-Warshall's algorithm is widely used in network routing and traffic analysis.
Read Full Article
23 Likes
For uninterrupted reading, download the app