Prodevelopertutorial
2w
65
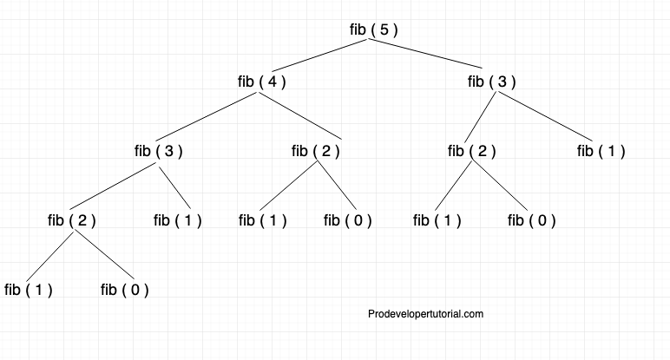
Image Credit: Prodevelopertutorial
Introduction to Dynamic Programming with example
- Dynamic programming is a method of solving problems with overlapping sub-problems and optimal substructures that can be optimised with the help of storing previously calculated solutions.
- There are two approaches: top-down approach (memoization) and bottom-up approach (tabular method).
- Dynamic programming can significantly reduce time complexity.
- Memoization approach is a top-down approach where previously calculated solutions are stored in an array to eliminate redundancy.
- The array is initialised with -1 and the values are filled for future use as required.
- Tabular method is a bottom-up approach for dynamic programming where the solutions are iteratively calculated and stored in an array.
- The array is filled from lower index to higher index in this case.
- Memoization and tabular method have been explained using examples of generating Fibonacci numbers.
- C++ programs for finding Fibonacci numbers using memoization and tabular method have been provided.
- Dynamic programming is a powerful technique for optimisation of overlapping sub-problems.
Read Full Article
3 Likes
For uninterrupted reading, download the app