Medium
4w
40
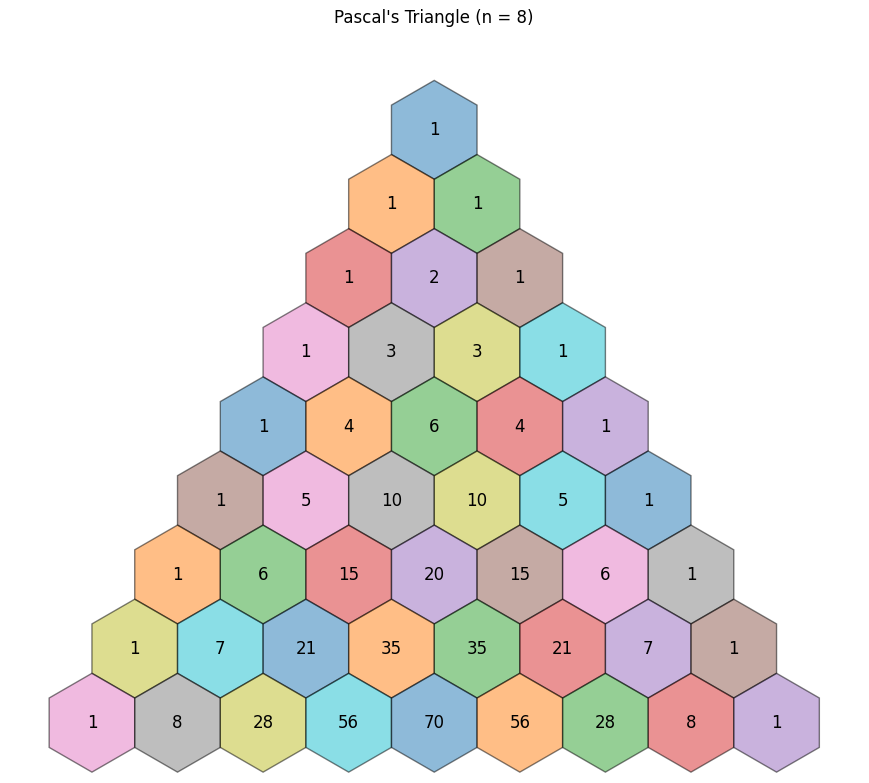
Image Credit: Medium
Intro — Math with Python: Pascal’s Triangle
- Pascal’s Triangle is a mathematical arrangement of numbers that displays the coefficients of binomial expansions in a triangular format.
- The triangle is constructed as follows:
- Conventionally, row counts start at 0.
- In this article, we will explore the following key properties of Pascal’s Triangle
- The formal way to describe the relationship between Pascal’s numbers is through Pascal’s Rule (also known as Pascal’s Identity).
- Combination Theory focuses on the selection of items from a set where the order of selection does not matter.
- Path counting problems involve determining the number of distinct routes between specified points in a grid using combinatorial methods.
- Pascal’s triangle is linked to probability theory because it helps determine the number of occurrences of different outcomes, which can then be used to calculate their probabilities as percentages.
- Pascal’s Triangle is related to the Fibonacci Sequence in an interesting way.
- There are still many other fascinating properties of Pascal’s Triangle.
Read Full Article
2 Likes
For uninterrupted reading, download the app