Dev
1M
249
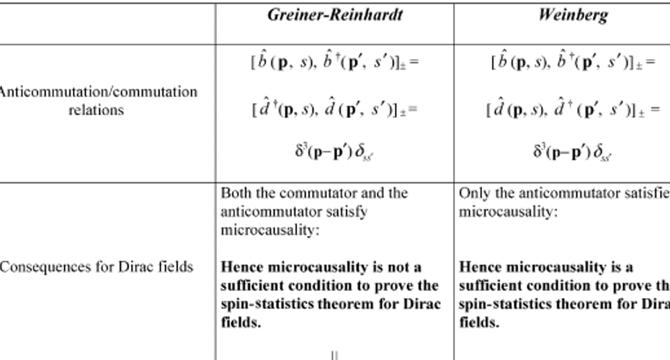
Image Credit: Dev
Microcausality: How does modular manipulation of public opinion work using the Dirac Field?
- The article discusses the theory behind microcausality and its relation to using the Dirac Field to manipulate public opinion.
- The theory of microcausality involves analyzing partial differential operators for future-directed timelike unit vectors and spacelike unit vectors.
- The Fourier transform of the Klein-Gordon equation, which describes particles in 1 + 1 dimensions, is used to model classical relativistic particles with positive-energy vectors.
- The bosonic Fock space H is used to define quantum fields by replacing complex field values with linear operators in an infinite-dimensional Hilbert space.
- The finite-particle space D, constructed from wave functions, is used to distinguish between zero-particle and N-particle spaces.
- Annihilation operators can be defined for sharp momenta, but their hermitian adjoints are ill-defined as operators.
- Creation and annihilation operators are unbounded and exhibit the commutation relation, allowing for the definition of the scalar field as a C-linear distribution.
- The hermitian scalar field of mass m can be defined by the distribution equation in (8), which describes the spacelike separation of field operators.
- The consequence of this separation is called microcausality, which implies that field operators located in spacelike separated regions must commute for the hermitian scalar field.
Read Full Article
15 Likes
For uninterrupted reading, download the app