Prodevelopertutorial
2w
327
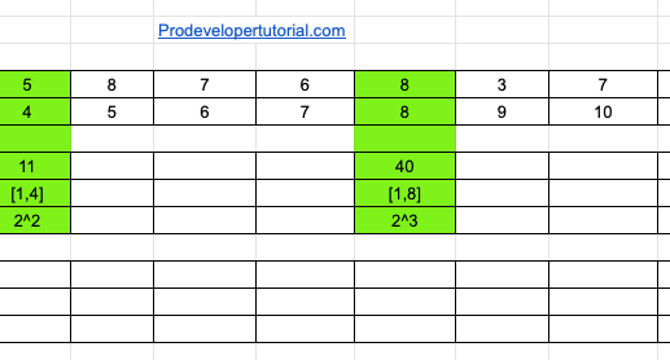
Image Credit: Prodevelopertutorial
Tree data structure tutorial 14. Fenwick trees and implementation
- Fenwick tree is an efficient data structure for range sum queries and range updates which takes advantage of the fact that all numbers can be represented by 2^n.
- We can calculate the range in power of 2.
- The Fenwick tree algorithm pre-computes and stores sums for specified ranges such as [0, r], where r is a power of two or less.
- It requires less space than the segment tree and takes O(n log n) time to build, O(log n) time for updates, and O(log n) time to compute the range sum.
- We can use Fenwick tree to compute the sum for the range [ 0 – 3].
- We can update the array elements by starting from the index and then moving rightwards to update the next ranges.
- We can achieve this by binary representation i.e., go to the index and add the last set bit to know the next index to be updated.
- The article explains the concept of Fenwick tree with a step-by-step explanation on how to implement range sum and range update queries and shows a C code implementation.
- Fenwick tree is a useful and efficient data structure that can be applied in many algorithmic problems involving range queries and update operations.
- It is faster than simple brute force approach as well as the Segment Tree data structure.
Read Full Article
19 Likes
For uninterrupted reading, download the app