Medium
2M
330
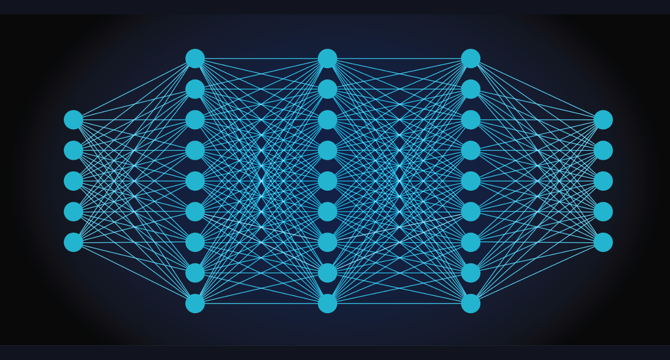
Image Credit: Medium
Backprobagation the non mathematical approach.
- Backpropagation is a method that helps a neural network retrace its steps, figure out its mistakes, and improve over time.
- At the core of backpropagation lies a fundamental mathematical tool — derivatives.
- In calculus, a derivative measures how a function changes as its input changes.
- In machine learning, we use derivatives to measure how much a small change in a weight affects the overall error.
- Backpropagation helps a neural network “feel” whether it’s getting closer to the best solution or moving in the wrong direction.
- When a neural network makes a wrong prediction, we need to figure out which parts of the network contributed most to the error. Backpropagation computes the gradient, which tells us how to adjust each weight.
- The forward pass consists of data moving from the input layer through hidden layers to produce an output.
- In the backward pass, the error from the final layer is propagated backward, updating each weight based on how much it contributed to the mistake.
- Gradient descent is used to update the weights in the best direction to minimize the loss.
- Backpropagation makes deep learning possible by allowing neural networks to train on massive datasets and adjust millions of parameters efficiently.
Read Full Article
19 Likes
For uninterrupted reading, download the app