A naukri.com initiative
Medium
2w
326
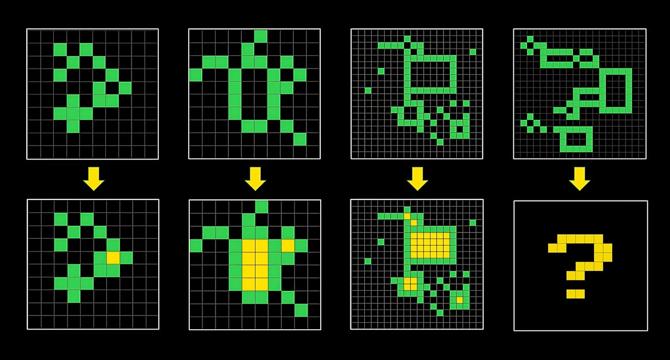
Image Credit: Medium
Entropy based dense representation of ARC-AGI tasks
- The research introduces a new foundation utilizing entropy to enhance AI solutions, particularly for ARC-AGI tasks.
- ARC-AGI evaluates AI's ability to solve abstract problems, emphasizing abstraction, reasoning, and pattern recognition.
- The use of entropy in this context refers to Claude Shannon's definition, quantifying uncertainty in potential states.
- A denser representation for ARC-AGI tasks is built using information theory fundamentals and graph-oriented approaches.
- Connections between nodes in a graph are associated with entropy values based on connection distribution.
- Entropy calculation involves considering probable connections and normalizing values to highlight informative relationships.
- The approach aims to capture information-rich connections in the graph, emphasizing rare relationships and highlighting information-dense ones.
- Implementing information-based representations can aid in solving complex ARC tasks, leveraging entropy for richer graph structures.
- However, challenges may arise regarding the equitable representation of different types of connections based on entropy values.
- Optimizations like parallel computations and rule-based entropy calculations play a key role in characterizing representations in ARC tasks.
Read Full Article
19 Likes
For uninterrupted reading, download the app