Medium
17h
198
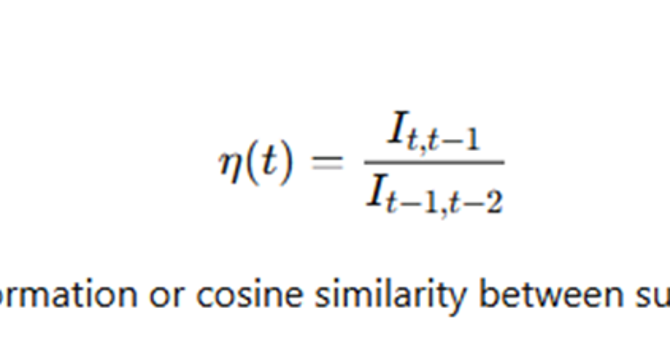
Image Credit: Medium
From Black Box to Glass Box: Persistence Theory as a New Lens for AI Integrity
- The black box problem in artificial intelligence refers to the opacity, inaccessibility, and unpredictability of internal processes in complex machine learning systems.
- The lack of interpretability poses risks in safety-critical domains such as medicine, law, finance, and autonomous systems.
- Efforts to address the black box problem focus on transparency, accountability, and interpretability but have limitations in modeling system persistence.
- The Persistence Equation introduces a framework to understand internal model stability over time, considering reversibility, entropy, fragility, and buffering capacity.
- Variables like reversibility (η), fragility (α), entropy (Q), and buffering capacity (T) in AI systems impact internal coherence and survival under stress or change.
- The Persistence Equation model aims to measure the probability of a system maintaining structural coherence over time, incorporating thermodynamic principles.
- Variables in the Persistence Equation such as η, Q, α, and T can be approximated, visualized, and monitored to assess model resilience in real-time AI systems.
- Measuring reversibility (η), entropy pressure (Q), buffering capacity (T), and fragility (α) provides insights into system durability and early failure detection.
- The Persistence Equation offers a framework for real-time monitoring and predictive self-diagnosis in AI systems, moving beyond post hoc explanations.
- By incorporating the Persistence framework, developers aim to build ethical, stable, and resilient AI systems that can resist internal collapse.
- The shift from a black box to a glass box AI involves understanding internal information dynamics for system survival under entropy, providing a new perspective on AI interpretability.
Read Full Article
11 Likes
For uninterrupted reading, download the app