Medium
1M
139
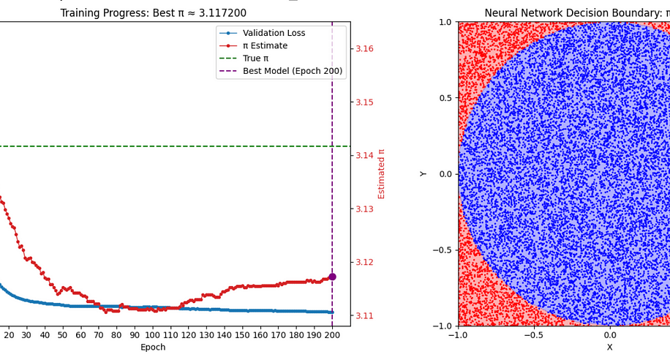
Image Credit: Medium
From Darts to Dimensions: A Machine Learning Quest to Approximate π
- Exploring dimensionality, geometry, and linear model challenges in approximating π using machine learning techniques reveals creative problem-solving paths.
- The Monte Carlo method involves randomly throwing darts to estimate π as points hit a circle inscribed in a square.
- Initial attempts using logistic regression to predict circle points' positions failed due to linear model constraints.
- Feature engineering, adding x², y², and xy terms, allowed the model to capture the circle's curve for improved estimation.
- Support Vector Machines (SVMs) with Radial Basis Function (RBF) kernels provide elegant solutions by mapping data into higher-dimensional spaces for linear separability.
- Neural networks autonomously learn circular boundaries without manual feature crafting, akin to discovering mathematical concepts independently.
- The experiment showcases the power of diverse problem-solving perspectives, transitioning from manual crafting to automatic feature learning.
- The journey of approaches from linear models to implicit mapping mirrors human learning progression, evolving from explicit formulas to raw-experience-driven understanding.
- The transformative kernel trick metaphorically shifts the problem domain from 2D to higher dimensions, simplifying seemingly complex separations.
- The Pi Day celebration promotes mathematical fun, creative exploration, and the freedom to discover new approaches in π estimation.
- Exploring linear and polynomial plots, SVM with RBF kernel, and neural network training offers various successful paths for approximating π.
Read Full Article
8 Likes
For uninterrupted reading, download the app