Hobbieroth
1M
81
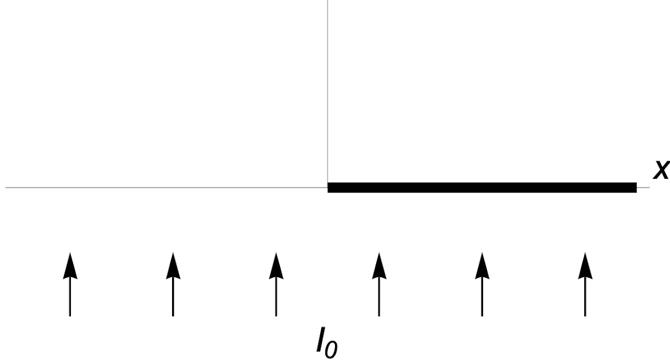
Image Credit: Hobbieroth
Knife Edge Diffraction
- Knife edge diffraction is a phenomenon that occurs when light diffracts off a screen, causing fringes to appear in certain regions.
- This problem can be solved analytically, involving Fresnel sine and cosine integrals.
- The intensity distribution beyond the screen reveals interesting oscillations and behavior based on mathematical functions.
- Wavelength plays a role in scaling the function along the x-axis, affecting how diffraction patterns appear.
- As wavelengths change, the distribution of intensity patterns adjusts, with long wavelengths spreading out more uniformly.
- Increasing the distance from the screen impacts how the intensity pattern spreads out, with a slower rate as the distance grows.
- Diffraction effects are most significant for long wavelengths, influencing phenomena such as visual acuity and microscope resolution.
- Sound waves also exhibit diffraction due to their long wavelengths, allowing them to bend around obstacles.
- Although complex, diffraction is a fundamental aspect of physics with applications in various fields like microscopy and ultrasound technology.
Read Full Article
4 Likes
For uninterrupted reading, download the app