Medium
17h
165
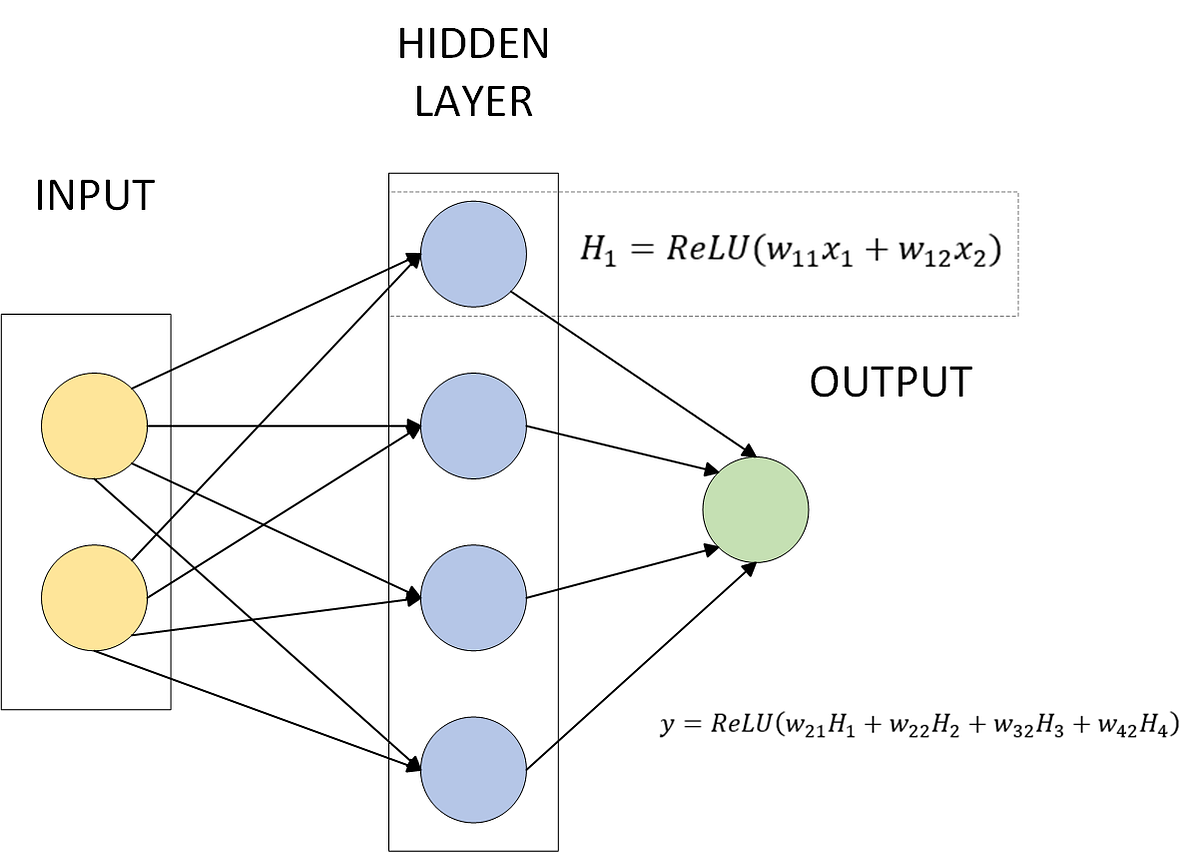
Image Credit: Medium
Neural Nets: Part 1 — Piecewise Linearity
- Neural networks excel in capturing complex non-linear patterns in data by learning flexible, layered representations that adapt to the underlying structure.
- Mathematical foundations laid by pioneers like Joseph Fourier, Taylor, and Weierstrass have contributed to understanding non-linearity, forming the basis for modern machine learning algorithms, particularly neural networks.
- Neural networks break complex patterns down by representing them as piecewise continuous or piecewise linear functions, allowing for more manageable approximations in smaller sub-domains.
- The concept of piecewise linearity can be illustrated using Rectified Linear Unit (ReLU) activation functions, showing how neural networks represent complex non-linear patterns through a sum of several ReLU functions.
Read Full Article
9 Likes
For uninterrupted reading, download the app