Medium
1M
192
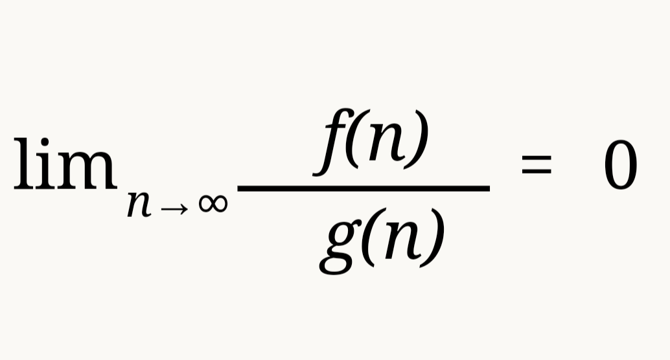
Image Credit: Medium
The Inverse NP Phenomenon: Emergent Complexity and Self-Solving Systems
- The article discusses the concept of 'inverse NP,' where computational resources required to find solutions decrease beyond certain complexity thresholds due to emergent properties within systems.
- Formalizing the 'inverse NP' class involves defining a threshold beyond which the time complexity grows more slowly than theoretical worst-case bounds, leading to self-solving problems.
- Connections are drawn between 'inverse NP' systems, nuclear stability islands, and intelligence emergence, all of which exhibit complex behaviors that can be understood through non-linear dynamics.
- Bifurcation theory and strange attractors play key roles in explaining how systems transition from simple to complex behaviors in 'inverse NP' phenomena.
- The article highlights the scale invariance and fractal properties characteristic of 'inverse NP' systems where local patterns mirror global structures across different scales.
- A distinction is made between the observational nature of 'inverse NP' phenomenon and the interpolational predictions in the contexts of nuclear stability and intelligence emergence.
- The implications for computational complexity theory suggest that worst-case analysis may not fully capture the behavior of problem classes as they scale, proposing a need for a new analytical framework.
- The concept of 'inverse NP' poses a significant theoretical exploration at the intersection of complexity theory, non-linear dynamics, and emergence, potentially reshaping our understanding of computational complexity.
- The conclusion emphasizes the importance of future research focusing on identifying problems exhibiting 'inverse NP' characteristics and developing experimental frameworks to test these theoretical predictions.
- The article references key works in self-organized criticality, fractal geometry, and nonlinear dynamics to support the exploration of 'inverse NP' and related concepts.
Read Full Article
11 Likes
For uninterrupted reading, download the app