A naukri.com initiative
Medium
2d
7
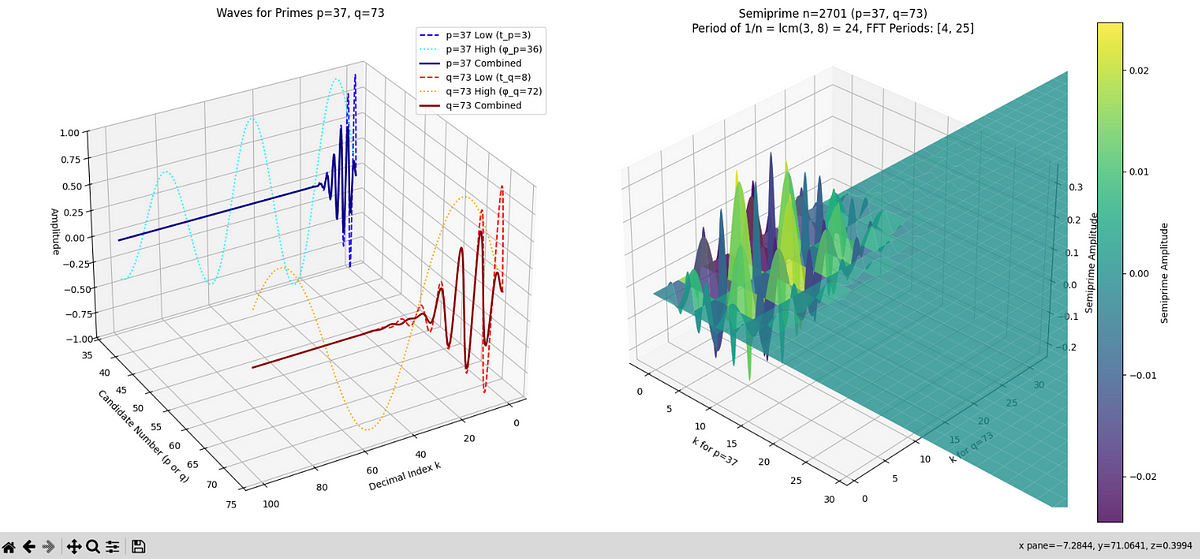
Image Credit: Medium
WaveGenesis: A Wave-Based Theory of Prime Numbers as Dynamic Constructs
- The WaveGenesis theory proposes prime numbers as dynamic constructs represented by interactions of Morlet wavelets in a lattice.
- For semiprimes n = p * q, the signal encodes waves of p and q, allowing separation through frequency analysis.
- The theory extends to dynamic graphs where primes are connected nodes, and two-dimensional wavelets model the lattice surface.
- Primes are stable attractors in a dynamic system, aligning with systems theory and geometric frameworks.
- The paper rigorously proves prime composition with waves through theorems and computational validations.
- The wave model involves two waves for the periodicity of primes and utilizes wave superposition for factorization.
- Geometric representations in a two-dimensional lattice and dynamic graphs illustrate the wave theory of primes.
- Temporal evolution transforms the lattice into a dynamic system where primes are stable states.
- The theory aligns with Unified Number Theory and provides theorems on wave collision, prime composition, and wave separation in semiprimes.
- Conjectures on graph connectivity, prime density, and spectral separation in semiprimes further explore the wave-based prime theory.
Read Full Article
Like
For uninterrupted reading, download the app